Viola da Gamba
physical modelling and experimental measurements
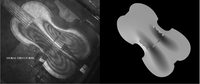
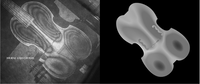
Physical modeling simulations can be used to analyze the vibrational behavior of a musical instrument. The fact that the model parameters have a direct physical interpretation enables us to predict how changes in the material properties and geometry of an instrument will affect the radiated sound. The calculation of the bridge admittance and the acoustic efficiency of a bowed string instrument can reveal useful information about its vibrational characteristics. In this project, an early viola da gamba with an asymmetric top plate and without a sound post or bass bar has been modeled.
The numerical formulation of the governing equations is carried out using the finite element method. The computer simulation of the instrument shows that the proposed geometry strongly supports most of the playing regime. Comparison with an instrument with a symmetric top plate points to the superiority of the postulated asymmetric design. Furthermore, using a linear buckling analysis, the critical load that would damage the instrument can be computed and appears to be much greater than the forces applied due to the existing string tension. Finally, comparisons with the measured admittance of reconstructed instruments and with images obtained via laser interferometry can be used to fine-tune the physical model parameters and extract further information regarding the material properties of the instruments.
References
- V. Chatziioannou. Reconstruction of an early viola da gamba informed by physical modeling. The Journal of the Acoustical Society of America 145 (6), 3435-3442, 2019. https://doi.org/10.1121/1.5111135
- V. Chatziioannou. Computer-aided reconstruction of an early viola da gamba. Basler Jahrbuch für Historische Musikpraxis, 35-36:283–290, (2018). ISBN: 978-3-905786-14-9.
In collaboration with University of Early Music (SCB), funded by the Swiss State Secretariat for Education, Research and Innovation (SERI).